Предельная степень деформации при осадке |
\\ Статьи
Обработка металлов давлением всегда осуществляется с рядом ограничений, которые определяют предельные условия осуществления процесса. Данные ограничения зависят от множества факторов, основными из которых являются взаимодействие инструмента и заготовки и их механические свойства.
Предельными условиями осуществления осадки является пластичность обрабатываемого материала. В работе рассмотрена связь между продольной и поперечной деформации при осадке круглыми бойками, которая позволяет оценить предельные условия осуществления сложного процесса периодической прокатки, представленного сочетанием двух процессов прокатки и осадки.

Балакин Валерий Федорович
Заведующий кафедрой технологического проектирования
Доктор технических наук, профессор
Национальная металлургическая академия Украины
Белан Константин Сергеевич
Ассистент кафедры технологического проектирования
Национальная металлургическая академия Украины
Перчаник Виктор Владимирович
Национальная металлургическая академия Украины
В отличие от процессов прокатки, где предельная деформация определяется силовыми условиями контактного взаимодействия, предельные условия осадки характеризуются пластичностью материала. В работах[1, 2] М.А. Зайков и В.Н. Перетятько предложили оценивать пластичность величиной истинного октаэдрического сдвига, т.к. октаэдрическая площадка, одинаково ориентированная относительно трех главных напряжений, является как бы «усредняющей», отражающей различно ориентированные плоскости сдвигов поликристалла. Величина октаэдрического сдвига описывается уравнениями[3]:
 ; (1)
; (1)
где  – главная максимальная истинная деформация при растяжении цилиндрического образца длиной
– главная максимальная истинная деформация при растяжении цилиндрического образца длиной ![]() до длины
до длины ![]() ;
;
 – относительное сужение площади поперечного сечения цилиндрического образца F0 до площади F1 в момент разрушения.
– относительное сужение площади поперечного сечения цилиндрического образца F0 до площади F1 в момент разрушения.
Из уравнения (1) легко определяется связь между относительным сужением и максимальной истиной деформацией растяжения цилиндрического образца
 ; (2)
; (2)
где d0 и d1 – диаметры цилиндрического образца до и после деформации.
Для плоской схемы единичной ширины при b0 = b1 = 1 истинная деформация относительного сужения площади поперечного сечения
 ; (3)
; (3)
где h0 и h1 – высота плоского образца до и после деформации.
Соотношение между истинными и относительными деформациями применительно к процессам осадки[4]
 ; (4)
; (4)
 ; (5)
; (5)
где ![]() и
и ![]() – относительные деформации осадки и удлинения.
– относительные деформации осадки и удлинения.
Таким образом, сумма относительных деформаций приблизительно (с точностью до 10%) равна нулю
![]() ; (6)
; (6)
Деформация разрушения, в качестве которой для всех видов деформированного состояния принимается октаэдрический сдвиг, отвечающий соответствующей объемной схеме напряженного состояния, приводиться к линейной схеме нагружения с помощью показателя напряженного состояния в «соответственное состояние», представляющего отношение максимального главного напряжения к сопротивлению материала при одноосной схеме с той же степенью деформации[5].
Октаэдрический сдвиг и критерий напряженного состояния определяется авторами работы [3] через усредненные по деформируемому образцу деформации и напряжения. Например, для стандартных механических испытаний Зайков и Перетятько приводят формулу среднего показателя напряженного состояния при разрыве образца  . С нашей точки зрения для определения предельного состояния формоизменения с помощью стандартных испытаний на разрыв нет смысла усреднять деформацию осадки, а следует пользоваться максимальной поперечной деформацией при разрыве образца. В работе [5, стр.156] указано, что «…определения показателей пластичности… необходимо производить в тех зонах деформированного объема, где схема напряженного состояния наиболее жесткая», т.е. чем сильнее преобладание в схеме растягивающих напряжений.
. С нашей точки зрения для определения предельного состояния формоизменения с помощью стандартных испытаний на разрыв нет смысла усреднять деформацию осадки, а следует пользоваться максимальной поперечной деформацией при разрыве образца. В работе [5, стр.156] указано, что «…определения показателей пластичности… необходимо производить в тех зонах деформированного объема, где схема напряженного состояния наиболее жесткая», т.е. чем сильнее преобладание в схеме растягивающих напряжений.
Деформация осадки круглым бойком из неподвижного центра в сочетании с прокаткой характерна для процессов периодического формоизменения. Она происходит за счет увеличения радиуса валка при неподвижном центре его вращения и занимает область контакта за линией центров в мгновенном очаге плоской схемы, т.е. рабочий валок перекатываясь по деформируемой полосе как бы «раздувается» при этом.
Очень важно определить степень деформации за линией центров, т.е. в зоне чистой осадки. До линии центров идет процесс прокатки в сочетании с осадкой и, как отмечают некоторые специалисты[6] «прокатка представляет собой по существу процесс непрерывной осадки между вращающимися бойками: валки непрерывно подают сами себе в очаг деформации все новые порции материала, подвергаясь здесь пластическому сжатию».
Рассматривая мгновенный очаг деформации при периодическом формоизменении вполне логично рассуждать об остановленном процессе, в котором и зона прокатки до линии центров и зона осадки за линией центров характеризуется непрерывной осадкой вращающимися валками, положение и величина радиуса которых определяет величину деформации в остановленный условно момент. При этом деформации сжатия в зоне контакта не равномерны в отличии от деформации растяжения. Максимальная величина сжатия позиционируется линией центров мгновенного очага.
Для определения связи между продольной и поперечной деформацией полосы воспользуемся методом смещенных объемов (смещенных площадей в плоской схеме), которые не усредняют неравномерность деформации сжатия. Обратимся к рис. 1, который представляет момент деформации осадки полосы высотой h0 на величину Dh=h0-h1 и соответствующее этому моменту продольное удлинение Dl половины длины начального профиля круглым бойком радиусом r0, увеличивающимся в процессе осадки до величины r1 со скоростьюV.

Рис.1. Схема плоской осадки полосы круглым бойком из неподвижного центра
Смещенные за счет деформации площади S0 в зоне контакта АВ1А и S1 за границами АА1 контактной зоны равны между собой по принципу сплошности несжимаемого материала. Исходя из равенства S0=S1, нетрудно получить связь между продольной ![]() и максимальной поперечной
и максимальной поперечной  деформациями без усреднения за счет схемы напряженно-деформированного состояния
деформациями без усреднения за счет схемы напряженно-деформированного состояния
 ; (7)
; (7)
где β – половина центрального угла в градусной мере, ограничивающего зону контакта.
Применение радианной меры для малых центральных углов (β≤0,7рад) и смещенной площади
![]() ; (8)
; (8)
где d – половина дуги контакта сегмента,
Dh – высота сегмента
дает соотношение между продольной и поперечной деформациями
![]() ; (9)
; (9)
Следует отметить, что плоская схема осадки круглым бойком по форме напоминает профиль шейки при испытаниях на растяжение. В этом случае относительное сужение 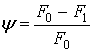 более правильно характеризует максимальную пластичность, чем относительное удлинение
более правильно характеризует максимальную пластичность, чем относительное удлинение  [7]. Например, механические свойства стали при температуре испытаний 20°С составляют[8]:
[7]. Например, механические свойства стали при температуре испытаний 20°С составляют[8]:
- для ферритной стали 20
e5 = 25%, y = 55%,
- для двухфазной стали 45
e5 = 16%, y = 40%.
При этом соотношение ![]() составляет 2,2 для стали 20 и 2,5 для стали 45.
составляет 2,2 для стали 20 и 2,5 для стали 45.
Уравнения (7) и (9) весьма полезны для определения предельной поперечной деформации при высоких температурах, т.к. справочная литература в большинстве своем характеризует только величину относительного удлинения e в момент разрыва образцов. Применение экспериментальных значений предельной степени деформации в сочетании с уравнением предельного состояния периодического формоизменения[9] позволяет определить максимальную величину подачи и оценить особенности калибровки технологического инструмента.
Выводы.
В отличии от процессов прокатки предельные условия осадки наступают только в результате исчерпания пластических свойств материала. В связи с тем, что данных по предельным условиям деформации мало, а в основном все справочные данные по пластичности получены на основании стандартных испытаний на разрыв. Для плоской схемы осадки круглыми бойками с использованием смещенных площадей получена связь между продольной и поперечной деформацией.
Перечень ссылок
1. Известия высших учебных заведений. Черная металлургия. – 1959. – №8. – С. 75-86.
2. Известия высших учебных заведений. Черная металлургия. – 1961. – №6. – С. 67-74.
3. Инженерные методы расчета технологических процессов обработки металлов давлением. М.: Металлургиздат, 1963, С. 412-416.
4. И. П. Громов. Теория обработки металлов давлением. М.: Металлургия, 1967, С. 45.
5. Сопротивление деформации и пластичность металлов. В.С. Смирнов, А.К. Григорьев, В.П. Пакудин, Б.В. Садовников. М.: Металлургия, 1975, С. 151.
6. В.С. Смирнов. Теория прокатки. М.: Металлургия, 1967, с. 149.
7. Металловедение и термообработка. Справочник. М.: Металлургиздат, 1961, С.22.
8. Марочник советских и зарубежных марок стали. М.: Промсырьеимпорт, 1976.
9. Балакин В.Ф., Белан К.С., Перчаник В.В. Предельные условия периодической прокатки//Теория и практика металлургии. – 2009. - №5-6, - С. 54-56.
Презентация
Контакты
Контакты
НАШІ КОНТАКТИ:
м. Дніпро
ISSN 20760507
Керівник проекту - Гриньов Володимир Анатолійович


