Автор: Vladimir Morkun, Natalia Morkun, Andrey Pikilnyak

Категории: automatization

The method and software based on this method for parameters estimation of the ultrasonic waves propagating in random heterogeneous medium are described
Key words: phased array, ultrasound, pulp, control, k-space

Simulation of high-energy ultrasound propagation in heterogeneous medium using k-space method

Vladimir Morkun
Vice-Rector for research, Doctor of Science, professor of Computer Science, Automation and Control Systems department
Kryvyi Rih National University

Natalia Morkun
PhD, Associate professor of Economic Cybernetics and Project Management Department
Kryvyi Rih National University

Andrey Pikilnyak
PhD- student of Computer systems and networks department, research assistant of the Computer Science, Automation and Control Systems department
Kryvyi Rih National University

Control of  mineral beneficiation process requires controlling the parameters of complex heterogeneous mediums, including solid, liquid and gas phases.
Ultrasonic oscillations are periodic disturbances of the elastic medium state, characterized by a change in its physical properties, which occur synchronously with perturbation. During ultrasonic propagation the local medium volume oscillations are transmitted to adjacent areas by means of elastic waves, characterized by a change in medium density in space and which transfer the fluctuations energy [1-3].
The basic relations describing ultrasonic oscillations and waves in the medium, follow from the equation of medium state, Newtonian equations of motion and the continuity equation [4,5]. The results are the wave-type equations that can be solved with appropriate initial and boundary conditions.
The equations of ultrasonic waves nonlinear propagation in heterogeneous medium can be derived from the mass, momentum, and energy conservation laws under the assumption of a quiescent, isotropic, and inviscid medium as follows[6,7]

, ,     (1)

where p is the acoustic pressure, ρ is the density, u is the particle velocity, ρ0 is the ambient density. The second order terms in (1) can be re-written in terms of the Lagrangian density by the repeated substitution of the acoustic equations in linearized form [8]. The Lagrangian density terms can be neglected as follows.

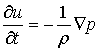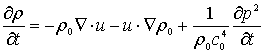, .                  (2)

Let’s neglect thermoviscous losses and include a phenomenological loss operator to account the arbitrary power law absorption [8], then the equation of state from the total pressure expansion using a Taylor series can be written as follows

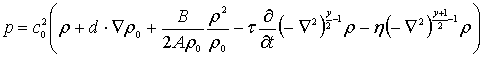,     (3)

where c0 is the isentropic sound speed, d is the particle displacement vector, and τ and η are the absorption and dispersion proportionality coefficients where  and . α is the acoustic absorption where , α0 is the absorption coefficient prefactor and y is the power law exponent [9].
The expressions given in (2) and (3) are the acoustic particle velocity, density, and pressure coupled set of equations.
Let’s combine these expressions into a single second order wave equation for the acoustic pressure. The modified Westervelt equation by neglecting higher order absorption, nonlinearity, and heterogeneity terms, can be written in the following form

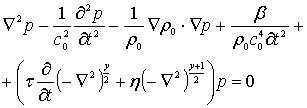,             (4)

where  is the nonlinearity coefficient.
By neglecting higher order absorption and nonlinearity effects, the conservation equations in (2) using a k-space method [10] can be written as follows

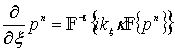
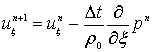                                                                              (5)

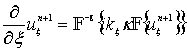
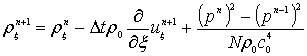
where i is the imaginary unit, kξ is the wavenumber in the  ξ direction, κ is the k-space adjustment where κ =sinc(c0kΔt/2), F and F−1 denote the forward and inverse Fourier transform, Δt is the time step.
The corresponding equation of state in discrete form is

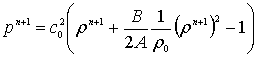,                       (6)

where the total density is given by and the discrete loss term is

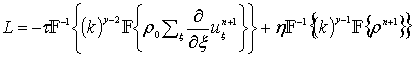,          (7)

Let's simulate the ultrasonic pressure field propagation in a heterogeneous medium using k-Wave toolbox (Matlab) which is designed for time domain ultrasound simulations in complex media like heterogeneous pulp. The simulation functions of this software are based on the k-space method and are both fast and easy to use [10].
The net pressure of all piezoelectric elements can be obtained by adding the effects of each source and written in the form

.                             (8)

Due to attenuation, the useful power at the point (x, y, z) is given by [11]

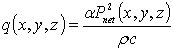,                                (9)

The total energy at a point (x, y, z) is given by

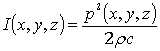,                         (10)

where  - intensity at the point (x, y, z), W/m.2
The results of the ultrasonic wave propagation through a heterogeneous medium with density kg/m3, for source strength of 1MPa and tone burst frequency of 1MHz for 16-element phased array with focus distance of 20mm are shown in Fig. 1. The central slice absorption distribution in grayscale as a background and the square of the pressure distribution on the surface of this background are shown.

Fig.1. Total beam pattern using maximum of recorded pressure
The final pressure field (a), the maximum pressure (b) and standard pressure (c) of the beam are shown on Fig. 2. The transducer focus and sidelobes are visible.

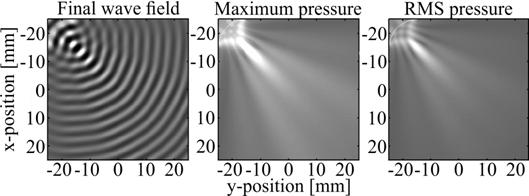
Fig. 2. Ultrasonic wave propagation in heterogeneous medium: a) the final pressure field, b) the maximum pressure c) the rms pressure

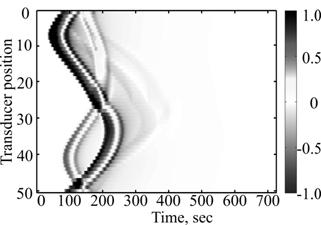
Fig. 3. The shape of the main wavefront
The linear cross-section of the focus in x direction is shown on Fig. 4: 1) for the single source; 2) simulation by k-space method in the water; 3) in a heterogeneous medium.

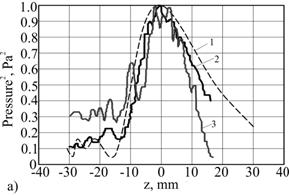
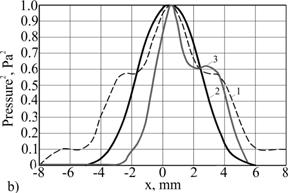
Fig. 4. The simulation results comparison of the normalized square of pressure for: 1) a simple screened source, 2) modeling by k-space method in a homogeneous medium (water) and 3) in the inhomogeneous medium (pulp) along the axis: a) - z and b) - x.
For the process of energy accumulation and transfer in a certain point of space can be given a numerical estimate by measuring the temperature. The simulation of temperatures was performed using the heat transfer equation [12]. The accumulated power was extracted from the three perpendicular lines that crossed the values of the simulated and measured ultrasound pressure focal area change (Fig. 5).

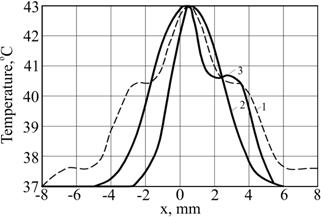
Fig. 5. The simulation results comparison of the temperature distribution for: 1) a simple screened source, 2) modeling by k-space method in a homogeneous medium (water) and 3) in the inhomogeneous medium (pulp) along the x axis.

Conclusions

To build a model of the ultrasonic field in a randomly inhomogeneous medium, the fiber spaces method (k-space), which increased the accuracy of parameter estimation field is used.

References

1. Morkun, V. Ultrasonic control of random heterogeneous mediums parameters.-Non Destructive Testing, ELSEVIER 92, (1991):989-993.
2. Morkun V. S., Morkun N. V,. Pikilnyak A.V. Ultrasonic facilities for the ground materials characteristics control, Metallurgical and Mining Industry, 2014, No2, p.p.31-35.
3. Morkun V. S., Morkun N. V,. Pikilnyak A.V. Modeling of ultrasonic waves propagation in inhomogeneous medium using fibered spaces method (k-space), Metallurgical and Mining Industry, 2014, No2, p.p. 43-48.
4. Morkun, V., Goncharov, S., Pikilnyak, A., Krivenko, A. Iron ore benefication processes optimization. ТЕKA. Commision of Motorization and Energetics in Agriculture 12, no.4 (2012): 162-166.
5. Morkun V. S., Morkun N. V,. Pikilnyak A.V. Iron ore flotation process control and optimization using high-energy ultrasound, Metallurgical and Mining Industry, 2014, No2. p.p. 36-42.
6. Morkun, V. Ultrasonic Control of Random Heterogeneous Mediums Parameters, AMMTIAC, no. 42(1992): http://ammtiac.alionscience.com/ammt/iacdocs.do?NT-49740.
7. Treeby B., Tumen M., Cox B. Time domain simulation of harmonic ultrasound images and beam patterns in 3D using the k-space pseudospectral method, MICCAI 2011, Part I, LNCS 6891, (2011): 363–370
8. Aanonsen, S., Barkve, T., Tjotta, J., Tjotta, S. Distortion and harmonic generation in the nearfield of a finite amplitude sound beam, J. Acoust. Soc. Am. 75, no.3, (1984):749–768.
9. Treeby, B., Cox, B. Modeling power law absorption and dispersion for acoustic propagation using the fractional Laplacian, J. Acoust. Soc. Am. 127, no.5, (2010):2741–2748
10. Internet resource: http://www.k-wave.org/
11. Seip, R., VanBaren, P., Cain, C., Ebbini, E. Noninvasive real-time multipoint temperature control for ultrasound phased array treatments, IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control 43, no.6, (1996): 1063-1073
12. Pennes H. H.Journal of Applied Physiology'1, 93 1948.